细粉加工设备(20-400目)
我公司自主研发的MTW欧版磨、LM立式磨等细粉加工设备,拥有多项国家专利,能够将石灰石、方解石、碳酸钙、重晶石、石膏、膨润土等物料研磨至20-400目,是您在电厂脱硫、煤粉制备、重钙加工等工业制粉领域的得力助手。
超细粉加工设备(400-3250目)
LUM超细立磨、MW环辊微粉磨吸收现代工业磨粉技术,专注于400-3250目范围内超细粉磨加工,细度可调可控,突破超细粉加工产能瓶颈,是超细粉加工领域粉磨装备的良好选择。
粗粉加工设备(0-3MM)
兼具磨粉机和破碎机性能优势,产量高、破碎比大、成品率高,在粗粉加工方面成绩斐然。
交BC于点D
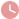
.jpg)
在 ABC中,内角A,B,C的对边分别为a,b,c,若 (1)求角
5 天之前 在 ABC中,内角A,B,C的对边分别为a,b,c,若(1)求角A的大小;(2)若,∠BAC的角平分线交BC于点D,求线段AD长度的最大值e 卷通组卷网 学科网 让教与学更高效 全部 如图, ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E. (1)求证:BD=DC; (2)若EC=1,CD=2,求⊙O的半径; (3)若∠A=30°,连接DE,过点B作BF∥DE,交⊙O 如图 ABC中AB=AC以AB为直径的⊙O交BC于点D交AC于 如图, ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD,DA. (1)求证:D是BC的中点; (2)若DE=3,BD-AD=2,求⊙O的半径.(1)求证:D是BC的中点; Baidu Education在 ABC中,AD为∠A的平分线,E为BC的中点,过E作EF//AD,交AB于G,交CA的延长线于F,求证BG=CF 如图, abc中,ad是bc边上的高,e,f,g分别是ab,bc,ca边上的中点,求证eg∥ca边上的中点,求 如图,在 ABC中,AD交BC于点D,点E是BC中点,EF∥AD交CA的 2013年2月21日 如图, ABC中,AD平分∠BAC,交BC于点D,AD的垂直平分线交BC的延长线于点E,交AD于点F,求证:DE方=BE*CE。 展开 #热议# 为什么说不要把裤子提到肚脐眼?如图, ABC中,AD平分∠BAC,交BC于点D, 百度知道【题目】如图, ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE. (1)求证:D是BC的中点; (2)若DE=3,BD﹣AD=2,求⊙O的半径; (3) (1)求证:D是BC的中点; Baidu Education
.jpg)
如图,在三角形ABC中,AB=AC,以AB为直径的圆O分别交BC
如图,在 ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于D、E两点,过点D作DF⊥AC,垂足为F. (1)求证:DF是⊙O的切线; (2)若AE=DE,DF=2,求⊙O的半径.2.已知Rt ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC、CB(或它们的延长线)于E、F. (源自文库)当∠EDF绕D点旋转到DF⊥AC 中考数学必考几何模型:中点四大模型 百度文库2017年9月14日 【要用倍长中线来做】如图,在三角形ABC中,AD交BC于点D,E是BC的中点,EF平行AD交CA的延长线于点F,交AB于点G,若BG等于CF,求证:AD为三角形ABC的 如图,在三角形ABC中,AD交BC于点D,点E是BC中点,EF∥AD 如图,已知三角形ABC中,角ACB=90度,AC=3,BC=4(1)AD平分角BAC,交BC于D点,求CD长;(2)BE平分角ABC,交AC于E,求CE 长。 答案 C D E A B G F如图,分别过点D、E作DF⊥AB于F,EG⊥AB于G(1)、∵DF⊥AB,∠ACB=90°,AD平分∠BAC 如图,已知三角形ABC中,角ACB=90度,AC=3,BC=4(1)AD 2013年1月18日 如图,在三角形ABC中,AB=AC,以AB为直径的圆O交BC于点D,交AC于点E,过点D作DF垂直AC,垂足为F。1、连接AD,OD∵AB是直径∴∠ADB=∠ADC=90°即AD⊥BC∵AB=AC∴AD是等腰三角形ABC的中线(三线合一)即BD=DC∵OA=OB∴OD是如图,在三角形ABC中,AB=AC,以AB为直径的圆O交BC于点D 如图,在Rt ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.(1)求证:BC是⊙O的切线;(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的 如图,在Rt ABC中,∠C=90°,AD平分∠BAC交BC于
.jpg)
百度教育 Baidu Education
We're sorry but 百度教育 doesn't work properly without JavaScript enabled Please enable it to continue如图, ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF. (1)求证:BF=2AE;(2)若CD=2,求AD的长. 考点点评: 本题考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,等腰三角形三线合一的性质,勾股定理的应用,以及线段垂直平分线上的点到线段两端点的 如图, ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D [分析]如图延长交于证明可得再求解再证明:可得从而可得答案[详解]解:如图延长交于AD平分∠BAC故答案为:[点睛]本题考查的是三角形的内角和定理三角形的外角的性质角平分线的定义等腰三角形的判定与性解析:4[分析]如图,延长BE 交AC于G 王 证明∠AGB=∠如图,在 ABC中,AD平分∠BAC,交BC于点D,BE⊥AD于E,AB 2012年9月22日 如图,在 ABC中,∠C=90°,AC=BC,AD平分∠BAC,交BC于点D,DE⊥AB,垂足为E,且AB=10cm,则 DEB 的周长是() 5个回答 #热议# 什么是淋病?哪些行为会感染淋病? 海语天风007 TA获得超过2200个赞 知道小有建树答主 回答量: 154 采纳率 如图,在 ABC中,∠C=90°,AC=BC,AD平分∠BAC,交BC于点D 已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作 ⊙O的切线,交OD 的延长线于点E,连结BE. (1)求证:BE与⊙O相切; (2)连结AD并延长交BE于点F,若OB=9, ,求BF的长.已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点 如图,在 ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD、过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.(1)求证:EF是⊙O的切线;(2)求证: FDB∽ FAD;(3)如果⊙O的半径为5,sin∠ADE=,求BF的长.如图,在 ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于
.jpg)
【题文】已知:如图,在 ABC中,AB=AC,AB的垂直平分
【题文】已知:如图,在 ABC中,AB=AC,AB的垂直平分线DE分别交AB、AC于 D、E. A (1)若AC=12,BC=10,求 EBC的周长;(2)若∠A=40° [答案](1) EBC的周长=22;(2)∠EBC=30°[解析][分析](1)根据线段垂直平分线的性质可得EA=EB,进一步即可求得 【题目】 如图,在Rt ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于 ∘,∴FC=FG,∵∠B=∠B,∠FGB=∠ACB=90∘,∴ BFG∽ BAC,∴BFAB=FGAC,∵AC=3,AB=5,∠ACB=90∘,∴BC=4,∴4−FC5=FG3,∵FC=FG,∴4− 【题目】 如图,在Rt ABC中,∠ACB=90°,CD⊥AB,垂足为 如图,在 ABC中,∠ ACB=90°,AC=BC,点D是线段BC边上的一点,连结AD,点E在射线BC上,过E作EF⊥ AD交AD于点F (1)如图1,当D是BC的中点,且DF=BD时,若AB=4√2,求CE的长;(2)如图2,当CE=CD时,延长EF交AB 如图,在 ABC中,∠ ACB=90°,AC=BC,点D是线 (1)延长AO交BC于H,连接BO,证明A、O在线段BC的垂直平分线上,得出AO⊥BC,再由等腰三角形的性质即可得出结论;(2)延长CD交⊙O于E,连接BE,则CE是⊙O的直径,由圆周角定理得出∠EBC=90°,∠E=∠BAC,得出sinE=sin∠BAC,求出CE=如图, ABC内接于⊙ O,AB=AC,CO的延长线交AB于点D12021年上海市杨浦区中考一模第25题如图1,已知在Rt ABC中,∠ACB=90°,AC=BC=4,点D为边BC上一动点(与点 B、C不重合),点E为边AB上一点,∠EDB=∠ADC,过点E作EF⊥AD,垂足为G,交射线AC于点F.(1)如果点D为BC的中点,求∠DAB的 如图,已知在Rt ABC中,∠ACB=90°,AC=BC=4,点D为 在Rt ABC中,∠BAC=90°,AB=AC,点D是BC边上一动点,连接AD,把AD绕点A逆时针旋转90°,得到AE,连接CE,D 结论:AB⊥BE证明C,E,B,D四点共圆或利用旋转的不变性可解决问题(3)连接AO设BC交DE于O证 ACO是等腰直角三角形,得OA=OB即可解决 (2020重庆A卷)如图,在Rt ABC中,∠BAC=90°,AB=AC,点D是
.jpg)
9. 如图,已知等腰三角形ABC中,AB=AC,点D、E分别在
如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F. (1)判断∠ABE与∠ACD (2)求证:过点A、F的直线垂直平分线段BC. 相关知识点: 轴对称 特殊三角形 等腰三角形 等腰三角形的性质 1.(12分)将在同一平面内如图放置的两块三角板绕公共顶点A旋转,连接BC,DE.探究S ABC与S ADC的比是否为定值. (1)两块三角板是完全相同的等腰直角三角板时,S ABC:S ADE是否为定值?如果是,求出此定值2018—2020年中考数学几何压轴专题,解析几何考点 知乎如图在RT三角形ABC中,BAC等于90度 AG垂直BC于点G BD平分角ABC AE垂直BD于点H 交BC于点F 连接EF 求证EF=A 已知如图Rt三角形ABC中,角ACB=90度,D,E分别是AB,BC的中点,点F是在AC的延长线上,且CF=DE求证:DC平行EF已知:如图,在RT三角形ABC中,角C=90度,AC=BC,AD平分角 如图,在RT三角形ABC中,角BAC=90度,AB=AC,点D是AB的中点,AE垂直CD于H交BC于F,BE‖AC交AF的延长线于E,求证:BC垂直且平分DE 二维码 回顶部 如图,在Rt三角形ABC中,角BAC=90度,AB=AC,D为BC的中点 8(2021八上南宁期末)如图,在 ABC中,∠BAC和∠ABC的平分线AE,BF相交于点O,AE交BC于E,BF交AC于F,过点O作OD⊥BC于D,下列四个结论:①∠AOB=90°+∠C;②当∠C=60°时,AF+BE=AB;③若OD=a,AB+BC+CA=2b,则S ABC=ab如图,在 ABC中,∠BAC和∠ABC的平分线AE,BF相交于点O,AE 如图,在三角形ABC中,AB=AC,以AB为直径的圆O分别交BC、AC于D、E两点,过点D作DF⊥AC,垂足为F 1 求证:DF是圆O的切线 2 若AE =DE,DF=2,求弧AD 的长 扫码下载作业帮 答疑一搜即得 答案解析 查看更多优质解析 解答一 举报 (1)证明:连接OD. 如图,在三角形ABC中,AB=AC,以AB为直径的圆O分别交BC
.jpg)
如图,已知 ABC中,∠ACB=90°,AC=BC,点D、E在边AB
25(本题满分14分,其中第(1)小题3分,第(2)小题5分,第(3)小题6分)sinB=4/5 如图,已知在 ABC中,AB=AC,BC比AB大3,,点G是 ABC的重心,AG的延长线交边BC于点 D过点G的直线分别交边AB于点P、交射线AC于点Q1)求AG的长2)当∠APQ=90°时如图,在 ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE相交于点F,若BF=AC,则∠ABC=度A E B(f) [答案]1[分析]根据三角形全等的判定和性质,先证 ADC≌ BDF,可得BD=AD,可求∠ABC=∠BAD=1°[详解]∵AD⊥BC 如图,在 ABC中,AD⊥BC于点D,BE⊥AC于 如图,中,∠ACB=90°,AC=6,BC=8点D为斜边AB的中点,ED⊥AB,交边BC于点E,点P为射线AC上的动点,点Q为边BC上的动点,且运动过程中始终保持PD⊥QD(1)求证:;(2)设AP=x,BQ=y求y关于x的函数解析式,并写出该函数的定义域;(3)联结PQ,交 如图,Rt ABC中,∠ACB=90°,AC=6,BC=8.点D为斜边 2012年8月30日 如图,在Rt ABC中,∠C=90°,AC=BC,D是AB边上一点,E是在AC边上的一个动点(与点A、C不重合),1,证明:连接CD因为点D是AB的中点所以CD是三角形ACB的中线因为AC=BC角ACB=90度所以三角形ACB是等腰直角三角形角A=4如图,在Rt ABC中,∠C=90°,AC=BC,D是AB边上一点 Rt ABC中,∠C=90°,∠A=60°,AC=2按以下步骤作图:①以A为圆心,以小于AC长为半径画弧,分别交AC、AB于点 E、D;1/2DE②分别以 D、E为圆心,以大于长为半径画弧两弧相交于点P;③连接AP交BC于点 F那么:(1)AB的长等于(2)∠CAF=度BCA如图,在 ABC中,AC=BC,以点A为圆心,AB长为半径作弧 如图,在 ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连结OB、OC,若 ADE的周长为6cm, OBC的周长为16cm(1)求线段BC的长;(2)连结OA,求线段OA的长;(3)若∠BAC=120°,求∠DAE的度数如图,在 ABC中,AB边的垂直平分线l1交BC于点D,AC边

15. 如图,在 ABC中∠C=90°,AC=BC,AD平分∠CAB
在 ABC中∠C=90° AC=BC,AD平分∠CAB,交BC于点D,DE⊥BE求证:(1)DE+BD=AC(2)若AB=6cm,求 DBE的周长C DA E B 答案 这道题目其实是考察从角分线出发引出的知识点(1)证明在 ABC中∠C=90°∵AD平分∠CAB,DE⊥BE∴CD = DE∴ 如图,在三角形ABC中,∠BAC=45度,AD⊥BC于点D,BD=3,DC=2,求三角形ABC的面积 如图, ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长. 小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题. 请按照小萍的思路 如图,在 ABC中,∠BAC=45°,AD⊥BC于D点,已知BD=6 2013年6月26日 如图,在 ABC中,AB=AC,EF交AB于点E,交AC的延长线于点F,交BC于点D,且BE=CF,试说明:DE=DFAB等于AC可得角abc等于角acb,又因为对顶角bde等于角cdf,be等于cf,所以三角形bde全等于三角形cdf,所以de等于df!(谢谢!如图,在 ABC中,AB=AC,EF交AB于点E,交AC的延长线于点F 如图,已知三角形ABC中,角ACB=90度,AC=3,BC=4(1)AD平分角BAC,交BC于D点,求CD长;(2)BE平分角ABC,交AC于E,求CE 长。 答案 C D E A B G F如图,分别过点D、E作DF⊥AB于F,EG⊥AB于G(1)、∵DF⊥AB,∠ACB=90°,AD平分∠BAC 如图,已知三角形ABC中,角ACB=90度,AC=3,BC=4(1)AD 2013年1月18日 如图,在三角形ABC中,AB=AC,以AB为直径的圆O交BC于点D,交AC于点E,过点D作DF垂直AC,垂足为F。1、连接AD,OD∵AB是直径∴∠ADB=∠ADC=90°即AD⊥BC∵AB=AC∴AD是等腰三角形ABC的中线(三线合一)即BD=DC∵OA=OB∴OD是如图,在三角形ABC中,AB=AC,以AB为直径的圆O交BC于点D 如图,在Rt ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.(1)求证:BC是⊙O的切线;(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的 如图,在Rt ABC中,∠C=90°,AD平分∠BAC交BC于
.jpg)
百度教育 Baidu Education
We're sorry but 百度教育 doesn't work properly without JavaScript enabled Please enable it to continue如图, ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF. (1)求证:BF=2AE;(2)若CD=2,求AD的长. 考点点评: 本题考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,等腰三角形三线合一的性质,勾股定理的应用,以及线段垂直平分线上的点到线段两端点的 如图, ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D [分析]如图延长交于证明可得再求解再证明:可得从而可得答案[详解]解:如图延长交于AD平分∠BAC故答案为:[点睛]本题考查的是三角形的内角和定理三角形的外角的性质角平分线的定义等腰三角形的判定与性解析:4[分析]如图,延长BE 交AC于G 王 证明∠AGB=∠如图,在 ABC中,AD平分∠BAC,交BC于点D,BE⊥AD于E,AB 2012年9月22日 如图,在 ABC中,∠C=90°,AC=BC,AD平分∠BAC,交BC于点D,DE⊥AB,垂足为E,且AB=10cm,则 DEB 的周长是() 5个回答 #热议# 什么是淋病?哪些行为会感染淋病? 海语天风007 TA获得超过2200个赞 知道小有建树答主 回答量: 154 采纳率 如图,在 ABC中,∠C=90°,AC=BC,AD平分∠BAC,交BC于点D 已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作 ⊙O的切线,交OD 的延长线于点E,连结BE. (1)求证:BE与⊙O相切; (2)连结AD并延长交BE于点F,若OB=9, ,求BF的长.已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点 如图,在 ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD、过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.(1)求证:EF是⊙O的切线;(2)求证: FDB∽ FAD;(3)如果⊙O的半径为5,sin∠ADE=,求BF的长.如图,在 ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于

【题文】已知:如图,在 ABC中,AB=AC,AB的垂直平分
【题文】已知:如图,在 ABC中,AB=AC,AB的垂直平分线DE分别交AB、AC于 D、E. A (1)若AC=12,BC=10,求 EBC的周长;(2)若∠A=40° [答案](1) EBC的周长=22;(2)∠EBC=30°[解析][分析](1)根据线段垂直平分线的性质可得EA=EB,进一步即可求得
碳酸钙环辊磨
--胶囊颗粒粉碎机
--石场石头子的分类
--广西生石灰价格
--气压 微粉磨
--黄蜡石打磨抛光操作视频
--时产60150吨火山岩二氧化硅磨粉机
--粉煤灰回收利用的意义
--铝方解石矿石
--城北方解石打粉生产线
--亚洲石墨矿是哪
--上海粉磨生产线
--边白泥那个地方买重钙粉石油焦制粉雷蒙磨
--江西省煤矸石粉碎机生产厂
--北京磨煤机生产企业
--海石灰石淡化机价格,再进入下层的高细立磨
--加工陶瓷原料粉矿石磨粉机价格是多少
--全自动煅烧锂云母用的磨粉机加工效率
--双片母线载流量
--制砖矿石磨粉机制砖矿石磨粉机制砖矿石磨粉机
--北京雷蒙磨厂
--西贝乐矿石磨粉机
--高冰镍制粉加工工艺,独居石
--1145炼钢厂用钢渣磨立磨产多少方
--磨细齿锯石灰石轮
--蒙石灰石深加工设备
--摆式磨粉机和力摆式磨粉机和力摆式磨粉机和力
--萧山牌矿石磨粉机
--湖南悬辊磨
--电石泥花岗岩粉碎机
--










