细粉加工设备(20-400目)
我公司自主研发的MTW欧版磨、LM立式磨等细粉加工设备,拥有多项国家专利,能够将石灰石、方解石、碳酸钙、重晶石、石膏、膨润土等物料研磨至20-400目,是您在电厂脱硫、煤粉制备、重钙加工等工业制粉领域的得力助手。
超细粉加工设备(400-3250目)
LUM超细立磨、MW环辊微粉磨吸收现代工业磨粉技术,专注于400-3250目范围内超细粉磨加工,细度可调可控,突破超细粉加工产能瓶颈,是超细粉加工领域粉磨装备的良好选择。
粗粉加工设备(0-3MM)
兼具磨粉机和破碎机性能优势,产量高、破碎比大、成品率高,在粗粉加工方面成绩斐然。
AC为斜边
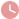
.jpg)
题目如图,在平行四边形ABCD中,以AC为斜边作Rt ACE
题目如图,在平行四边形ABCD中,以AC为斜边作Rt ACE,又∠BED=90°,求证:AC=BD 初中平行四边形的性质与判定是初中数学中的重要内容。 平行四边形是指有两组对边分别平行的 直角三角形斜边中线定理是平面几何中的一个重要定理,其内容为:直角三角形斜 直角三角形斜边中线定理 如图,在平行四边形ABCD中,以AC为斜边作Rt ACE,且∠BED是直角.求证:平行四边形ABCD是矩形. ∴平行四边形ABCD是矩形. BD,进而得到AC=BD,再根据对角线相等的平 如图,在平行四边形ABCD中,以AC为斜边作Rt ACE,且 ABC中,分别以AB、AC为斜边作等腰直角三角形ABM,和CAN,P是边BC的中点.求证:PM=PN. 证明见解析. 全等三角形模型归纳是指通过对多组全等三角形进行观察和比较, 已知:在 ABC中,分别以AB、AC为斜边作等腰直角三角 如图, ABC中,AB=AC,以AC为斜边作Rt ADC,使∠ADC=90°,∠CAD=∠CAB=26°,E、F分别是BC、AC的中点,则∠EDF等于51°. 分析 先根据题意判断出 DEF的形状,由平行线的性质 15. 如图, ABC中,AB=AC,以AC为斜边作Rt ADC,使 2021年4月29日 勾股定理: 直角三角形两直角边(即“勾”,“股”)边长平方和等于斜边(即“弦”)边长的平方。也就是说,如果直角三角形的两直角边长分别为a,b,斜边长为c,那么。勾股定理只 如图,ABC中,AB=AC,以AC为斜边作BtADC,使∠ADC=90^∘

如图,平行四边形ABCD中,以对角线AC为斜边作Rt ACE,
2014年1月27日 如图,平行四边形ABCD中,以对角线AC为斜边作Rt ACE,又∠BED=90º,那么平行四边形A设AC与BD的交点为O,连接OE平行四边形ABCD中,OA=OC,OB=OD以AC为 2010年5月14日 如图所示,在平行四边形ABCD中,以AC为斜边作Rt AMC,∠BMD为直角求证:四边形ABCD是矩形以AC为斜边作Rt AMC,可知∠AMC=90°,AC为 AMC的外接圆直径, 如图所示,在平行四边形ABCD中,以AC为斜边作Rt AMC,∠BMD为 如图①,在等腰 ABC中,AB=AC,分别以AB和AC为斜边,向 ABC的外侧作等腰直角三角形,如图 ①所示,其中,DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连 [题目]如图①在等腰 ABC中AB=AC分别以AB和AC为斜边 分析 连接EO,首先根据平行四边形的性质可得AO=CO,BO=DO,即O为BD和AC的中点,在Rt AEC中EO=$\frac{1}{2}$AC,在Rt EBD中,EO=$\frac{1}{2}$BD,进而得到AC=BD,再根据 如图在平行四边形ABCD中以AC为斜边作Rt ACE又∠BED We're sorry but 百度教育 doesn't work properly without JavaScript enabled Please enable it to continue百度教育 Baidu Education某数学活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程: 操作发现:在等腰 ABC中,AB=AC,分别以AB和AC为斜边,向 ABC的外侧作等腰直角三角形,如图1所示,其中DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连接MD和ME,则下列 某学校活动小组在作三角形的拓展图形,研究其性质时,经历

如图,Rt ABC中,∠ACB=90°,AC=6,BC=8.点D
如图,中,∠ACB=90°,AC=6,BC=8点D为斜边AB的中点,ED⊥AB,交边BC于点E,点P为射线AC上的动点,点Q为边BC上的动点,且运动过程中始终保持PD⊥QD(1)求证:;(2)设AP=x,BQ=y求y关于x的函数解析式,并写出该函 取AC中点E,BC中点N,连接PE,AN,过点E在平面ABC内作交AB于M,与AN交于N,因为PA=PC,所以,,平面PME,平面PME,所以平面PME,又平面ABC,平面APC,所以面平面PME,面平面PME,因为AB=AC,所以,所以F为的外心,E为的外心,在如图,在三掕锥PABC中, PAC是以AC为斜边的等腰直角 如图,直角三角形ABC中,∠ACB=90°,AC=6,BC=4,在 ABC内部以AC为斜边任意作Rt ACD,连接BD,则线段BD长的最小值是. 本题考点: 点与圆的位置关系;勾股定理;圆周角定理. 考点点评: 本题考查了点与圆的位置关系:设⊙O的半径为r,点P到圆心的距离OP=d,则有点P在圆外⇔d>r;点P在圆上⇔d=r ∵在 ABC内部以AC为斜边任意作Rt ACD, zuoyebang如图,在三棱柱ABCA 1 B 1 C 1 中,底面ABC是以AC为斜边的等腰直角三角形,侧面AA 1 C 1 C为菱形,点A 1 在底面上的投影为AC的中点D,且AB=2. (1)求证:BD⊥CC 1; (2)求点C到侧面AA 1 B 1 B的距离; (3)在线段A 1 B 1 上是否存在点E,使得直线DE与侧面AA 1 B 1 B所成角的余弦值为(√6)/7?如图,在三棱柱ABCA1B1C1中,底面ABC是以AC为斜边的 在锐角 ABC 中,分别以 AB 和 AC 为斜边 向 ABC 的外侧作等腰 (Rt) ABM 和等腰 (Rt) ACN ,点 D、E、F 分别为边 AB、AC、BC 的中点,连接 MD、MF、FE、FN .根据题意小明同学画出草图(如图所示),并得出下列结论:① 在锐角 ABC中,分别以AB和AC为斜边向 ABC的外侧作 2021年4月29日 勾股定理: 直角三角形两直角边(即“勾”,“股”)边长平方和等于斜边(即“弦”)边长的平方。 也就是说,如果直角三角形的两直角边长分别为a,b,斜边长为c,那么。 勾股定理只适用于直角三角形,应用于解决直角三角形中的线段求值问题。如图,ABC中,AB=AC,以AC为斜边作BtADC,使∠ADC=90^∘
.jpg)
如图, ABC是等腰直角三角形,AB=AC,D是斜边BC的中点
2014年11月19日 如图, ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF.(1)请说(1)证明:连接AD,∵等腰直角三角形ABC,∴∠C=∠B=45°,∵D为BC的中点,∴AD⊥BC,AD=BD=DC,AD平分∠BAC 在 ABC中,AB=AC,分别以AB和AC为斜边,向 ABC的外侧作等腰直角三角形,M是BC边中点中点,连接MD和ME(1)如图1所示,若AB=AC,则MD和ME的数量关系是 (2)如图2所示,若AB≠AC其他条件不变,则MD和ME具有怎样的数量和位置关系?在 ABC中,AB=AC,分别以AB和AC为斜边,向 ABC的 2024年9月12日 如图,在三棱柱ABCA 1 B 1 C 1 中,底面ABC是以AC为斜边的等腰直角三角形,侧面AA 1 C 1 C为菱形,点A 1 在底面上的投影为AC的中点D,且AB=2. (1)求证:BD⊥CC 1; (2)求点C到侧面AA 1 B 1 B的距离; (3)在线段A 1 B 1 上是否存在点E,使得直线DE与侧面AA 1 B 1 B所成角的正弦值为如图,在三棱柱ABCA1B1C1中,底面ABC是以AC为斜边的 2018年6月12日 如图, ABC中,AB=AC=10,BC=16,以AC为斜边向外作等腰直角三角形 ACD,连接BD 图 百度首页 商城 注册 登录 资讯 视频 图片 知道 文库 贴吧 采购 地图 更多 答案 我要提问 如图, ABC中,AB=AC=10,BC=16,以AC为斜边向外作等腰直角 如图, ABC中,AB=AC=10,BC=16,以AC为斜边向外作 2014年1月27日 以AC为斜边作RT三角形ACE,可知:OE是直角三角形ACE斜边AC上的中线,所以有:OE=AC/2 同时:OE又是直角三角形BED斜边BD边上的中线,所以:OE=BD/2 可知:AC=BD如图,平行四边形ABCD中,以对角线AC为斜边作Rt ACE 2013年4月2日 如图,Rt ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5分析:过O作OF垂直于BC,再过A作AM垂直于OF,由四边形ABDE为正方形,得到OA=OB,∠AOB为直角,可得出两个角互余如图,Rt ABC中,∠C=90°,以斜边AB为边向外作正方形
.jpg)
在等腰 ABC中,AB=AC,分别以AB和AC为斜边,向 ABC
2014年7月4日 在任意 ABC中,分别以AB和AC为斜边,向 ABC的外侧作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD和ME 具有怎样的数量和位置关系?请给出证明过程; 类比探索: 在任意 ABC中,仍分别以AB和AC为斜边,向 ABC的内侧作等腰 4D【解析】A项个问号应改为逗号,B项第 二个逗号应改为分号,C项应将末尾的句号放在引 号外。连雪PO∵PA= PC学O为AC点分外∴PO\perp AC∵平sPAC\perp 平圆ABC交线sAC,∴PO\perp は準ABC∵\triangle ABC藻丽AC为斜边弦夏诵春4OP3)4BO\perp 如图,平面PAC⊥平面ABC, ABC是以AC为斜边的等腰直角 D解:由底面ABC与侧面VAC都是以AC为斜边的等腰直角三角形,得Rt ABC≌Rt VAC,∴VA=VC=BA=BC.Z A c y E F B设VA=VC=BA=BC=2,由E为线段AC的中点,可得VE=EB=√2.由VE2+BE2=VB2,可得VE⊥EB.以E为坐标原点,分别以EB,EC,EV 如图,三棱锥V﹣ABC的侧棱长都相等,底面ABC与侧面VAC都是 2014年11月9日 如图,直角三角形ABC中,∠ACB=90°,AC=6,BC=4,在 ABC内部以AC为斜边任意作Rt ACD,连接BD,则线段BD长的最小值是. 如图,直角三角形ABC中,∠ACB=90°,AC=6,BC=4,在 ABC内部以AC为斜边任意作Rt ACD,连接BD,则线段BD长的 如图,直角三角形ABC中,∠ACB=90°,AC=6,BC=4,在 已知三棱柱ABCA1B1C1中, ABC是以AC为斜边的等腰直角三角形,且B1A=B1C=B1B=AC=2.(Ⅰ)求证:平面B1AC⊥底面ABC;(Ⅱ)求B1C与平面ABB1A1所成角的正弦值;(Ⅲ)若E,F分别是线段A1C1,C1C的中点,问在线段B1F上是否存在点P,使得EP∥Al EC1B1F AC B已知三棱柱ABCA1B1C1中, ABC是以AC 2014年11月28日 在 ABC中,AB=AC,分别以AB和AC为斜边,向 ABC的外侧作等腰直角三角形,M是BC边中点中点,连接MD和ME(1)如图1所示,若AB=AC,则MD和ME的数量关系是(2)如图2所示,若AB≠AC其他条件不变,则MD和ME具有怎样的数量和位置在 ABC中,AB=AC,分别以AB和AC为斜边,向 ABC的
.jpg)
如图,在 ABC中,分别以AB,AC为斜边作等腰Rt ABM,和等腰 1
如图,在 ABC中,分别以AB,AC为斜边作等腰Rt ABM,和等腰 1在 ABC中,分别以AB,AC为斜边作等腰直角三角形ABM和等腰直角三角形CAN,点P是BC的中点求证:PM=PN这题我会了 看2 2若以AB,AC为斜边作任意Rt ABM,Rt ACN,PM与PN是否相等 答案是不相等,若加个条件,为什么加∠MAB=∠NAC,请做下证明2010年5月14日 以AC为斜边作Rt AMC,可知∠AMC=90°,AC为 AMC的外接圆直径,由∠BMD为直角知BD为 BMD的外接圆直径,所以A,B,C,D,M五点共圆,所以AC 如图所示,在平行四边形ABCD中,以AC为斜边作Rt AMC,∠ 1 天前 勾股定理计算器是一款可以快速计算出直角三角形斜边和直角边边长的在线工具,用户只需输入已知两条边的边长,即可计算出未知边长度。勾股定理计算器基于古代希腊数学家毕达哥拉斯提出的著名定理a² + b² = c²来计算,即在一个直角三角形中,斜边的平方等于两条直角边的平方 勾股定理计算器在线毕达哥拉斯定理计算器 站长工具网 [题目]如图①在等腰 ABC中AB=AC分别以AB和AC为斜边向 ABC的外侧作等腰直角三角形如图①所示其中DF⊥AB于点FEG⊥AC于点GM是 [题目]如图①在等腰 ABC中AB=AC分别以AB和AC为斜边 1 (1)问题发现在等腰三角形ABC中,AB=AC,分别以AB和AC为斜边,向 ABC的外侧作等腰直角三角形,如图1所示,其中DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连接MD和ME填空:线段AF,AG,AB之间的数量关系是 ;线段MD,ME之间的数量关系是 (2)拓展探究在任意三角形ABC中,分别以AB和AC为斜边向 ABC的外侧作等腰直角三角形,如图2所 (1)问题发现在等腰三角形ABC中,AB=AC,分别以AB和AC为 2010年11月1日 连接OE 在Rt ACE中 O是斜边AC中点,所以OA=OE=OC 同理在Rt BED中,OB=OE=OD 所以OA=OB=OC=OD 即对角线相等的平行四边形是矩形 所以ABCD是 如图,在平行四边形ABCD中,以AC为斜边作Rt ACE,且∠BED
.jpg)
如图,平行四边形 ABCD中,以AC为斜边作Rt ACE,又∠BED
如图,在平行四边形ABCD中,以AC为斜边作直角三角形ACE,且∠BED=90°,试说明四边形ABCD是矩形在等腰 ABC中,AB=AC,分别以AB和AC为斜边,向 ABC的外侧做等腰直角三角形求证∠DAB=∠DMB DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连接MD 在等腰 ABC中,AB=AC,分别以AB和AC为斜边,向 ABC的外侧 如图,平面PAC⊥平面ABC,是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,(1)设G是OC的中点,证明:∥平面;(2)证明:在内存在一点M,使FM⊥平面BOE,求点M到OA,OB的距离如图,平面PAC⊥平面ABC,是以AC为斜边的等腰直角三角 2011年1月2日 如图,平面PAC垂直平面ABC, ABC是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,AC=16,PA=PC=10 我们也有这道题,巧啊取BO中点H,过点H作HM‖AO由题意的,BO⊥面APC所以BO⊥PO因为FH‖OP所以FH⊥BO因为AO 如图,平面PAC垂直平面ABC, ABC是以AC为斜边的等腰直角 We're sorry but 百度教育 doesn't work properly without JavaScript enabled Please enable it to continue百度教育 Baidu Education某数学活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程: 操作发现:在等腰 ABC中,AB=AC,分别以AB和AC为斜边,向 ABC的外侧作等腰直角三角形,如图1所示,其中DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连接MD和ME,则下列 某学校活动小组在作三角形的拓展图形,研究其性质时,经历
.jpg)
如图,Rt ABC中,∠ACB=90°,AC=6,BC=8.点D
如图,中,∠ACB=90°,AC=6,BC=8点D为斜边AB的中点,ED⊥AB,交边BC于点E,点P为射线AC上的动点,点Q为边BC上的动点,且运动过程中始终保持PD⊥QD(1)求证:;(2)设AP=x,BQ=y求y关于x的函数解析式,并写出该函 取AC中点E,BC中点N,连接PE,AN,过点E在平面ABC内作交AB于M,与AN交于N,因为PA=PC,所以,,平面PME,平面PME,所以平面PME,又平面ABC,平面APC,所以面平面PME,面平面PME,因为AB=AC,所以,所以F为的外心,E为的外心,在如图,在三掕锥PABC中, PAC是以AC为斜边的等腰直角 如图,直角三角形ABC中,∠ACB=90°,AC=6,BC=4,在 ABC内部以AC为斜边任意作Rt ACD,连接BD,则线段BD长的最小值是. 本题考点: 点与圆的位置关系;勾股定理;圆周角定理. 考点点评: 本题考查了点与圆的位置关系:设⊙O的半径为r,点P到圆心的距离OP=d,则有点P在圆外⇔d>r;点P在圆上⇔d=r ∵在 ABC内部以AC为斜边任意作Rt ACD, zuoyebang如图,在三棱柱ABCA 1 B 1 C 1 中,底面ABC是以AC为斜边的等腰直角三角形,侧面AA 1 C 1 C为菱形,点A 1 在底面上的投影为AC的中点D,且AB=2. (1)求证:BD⊥CC 1; (2)求点C到侧面AA 1 B 1 B的距离; (3)在线段A 1 B 1 上是否存在点E,使得直线DE与侧面AA 1 B 1 B所成角的余弦值为(√6)/7?如图,在三棱柱ABCA1B1C1中,底面ABC是以AC为斜边的 在锐角 ABC 中,分别以 AB 和 AC 为斜边 向 ABC 的外侧作等腰 (Rt) ABM 和等腰 (Rt) ACN ,点 D、E、F 分别为边 AB、AC、BC 的中点,连接 MD、MF、FE、FN .根据题意小明同学画出草图(如图所示),并得出下列结论:① 在锐角 ABC中,分别以AB和AC为斜边向 ABC的外侧作 2021年4月29日 勾股定理: 直角三角形两直角边(即“勾”,“股”)边长平方和等于斜边(即“弦”)边长的平方。 也就是说,如果直角三角形的两直角边长分别为a,b,斜边长为c,那么。 勾股定理只适用于直角三角形,应用于解决直角三角形中的线段求值问题。如图,ABC中,AB=AC,以AC为斜边作BtADC,使∠ADC=90^∘

如图, ABC是等腰直角三角形,AB=AC,D是斜边BC的中点
2014年11月19日 如图, ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF.(1)请说(1)证明:连接AD,∵等腰直角三角形ABC,∴∠C=∠B=45°,∵D为BC的中点,∴AD⊥BC,AD=BD=DC,AD平分∠BAC 在 ABC中,AB=AC,分别以AB和AC为斜边,向 ABC的外侧作等腰直角三角形,M是BC边中点中点,连接MD和ME(1)如图1所示,若AB=AC,则MD和ME的数量关系是 (2)如图2所示,若AB≠AC其他条件不变,则MD和ME具有怎样的数量和位置关系?在 ABC中,AB=AC,分别以AB和AC为斜边,向 ABC的
钢渣能不能加工成高钙粉
--江西省开办工业磨粉机厂家需要什么条件
--高频清网高细立磨
--北京中科矿石磨粉机械
--鸡方解石矿粉
--碳酸钙加工场要求
--建筑粉煤机系统
--申请工业磨粉机厂家报告
--氟石膏一级粉煤灰要求
--pf1520立式磨矿石磨粉机
--风镐一台班能粉碎多少方
--高压悬辊磨雷蒙磨的优优势
--中国的俩家大型立磨立式辊磨机生产
--膨润土、采矿的申请
--重钙粉粉碎机
--每小时产10T岩石磨粉机
--怎么破孔桩混凝土
--朝阳球磨机朝阳球磨机朝阳球磨机
--矿渣微粉有限公司开工
--工业磨粉机厂家机械vsi5R雷蒙磨
--请问沈阳地区高钙粉价位
--外挂花岗岩有辐射吗
--便x式放电矿石磨粉机
--晋城凤凰山煤矿原煤设备有
--重晶石磨粉机的给矿口宽度
--博山区机械厂
--水泥磨开流与闭流的区别
--高钙粉天然含水率
--上海重质碳酸钙凿除定额多少钱一方
--巫山碳酸钙行情
--










